책 "허수, 베리 마주르 지음" 에서 발견한 이 질문에 대해 조금 고민해보면, 생각보다 의심의 여지없는 답을 하는 것이 꽤 어렵다는 것을 알 수 있다. 왜냐하면 이 질문은 곱하기 음수가 무엇인지, 사람이 잘 알기 어려운 개념을 묻기 때문이다.
이 질문에 답을 하기 위해서는 수가 무엇인지 그것도 음수가 무엇인지 그리고 곱하기가 무엇인지에 대한 정확한 이해가 필요한데 대부분 그렇지 못하고, 이 질문을 처음 만났을때의 필자도 마찬가지였다.
수에 대한 정의에 있어서 필자는 다른 글에서 대칭체계의 부산물로서 설명한 적이 있고, 이 작업은 흥미롭게도 더 깊이 추상적으로 내려가볼 수 있다. 그러나 깨달은 것은 더 추상화하지 않더라도 직선상에 0이라는 점을 찍고 그 양쪽으로 한쪽은 1,2,3,4라는 양수, 그리고 반대쪽으로는 -1,-2,-3-4로 가는 음수로 정의해도 전체의 틀을 잡는데는 크게 부족하지 않다는 사실이다. 그리고 이러한 체계는 일단은 기본수학교육을 받은 모두가 익숙하다는 장점이 있다.
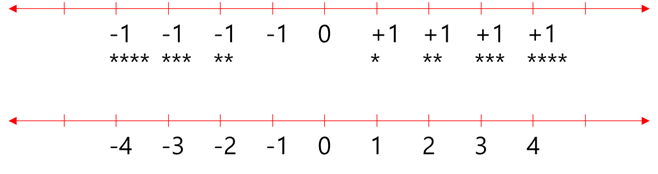
그러면 다시 처음 질문인 음수와 음수의 곱으로 돌아가보자.
음수란 양수의 대칭점에 있는 수이다. 방향이 다른 쪽으로 뻗어가며 곱하기란 "몇번을 반복해서 그쪽으로 이동하는 것인가"에 대한 연산이다. 특히 양수에 있어서는 이 정의들은 형태만 다르지 이견이 없게 잘 이해할 수 있다.
즉, A와 B를 양수라고 했을때, A * B 라는 것은 원점에서 A만큼의 이동을 B번 반복한다. 직관적으로 머리속에 잘 그려진다.
그러면 다음으로 -A * B는 무엇일까? 이것도 어렵지 않게 A의 대칭에 있는 -A로의 이동을 역시 B번 만큼 반복한다는 것으로 이해할 수 있다.
그런데 과연 A*-B, 즉 A를 -B라는 음수만큼 반복한다는 것은 어떤 의미일까? 결론적으로는 신기하게도 그 의미가 명확해서 음수곱하기 음수가 양수가 되는 것이 아니다. 사실은 대칭의 연산체계에서 유일하게 서로 모순이 없도록 정의할 수 있는 방법이 바로 음수곱하기 음수가 양수가 되도록 하는 방법이기 때문에 그렇게 된다.
이를 테면 곱셈의 교환법칙이나 결합법칙 등 우리가 사용하는 법칙을 양수와 음수 모두에서 만족시키는 방법은 아래 몇가지를 살펴봐도
-1 * A = -A
1 * -1 * A = -A
-1 * -1 * A = A
-1* (-1*A) = A
-1 * (-A) = A
바로 무언가의 음수 곱은, 앞의 수를 음수의 절대값만큼 반복한다음에 부호를 바꿔주는 방법 뿐이다. 그래야 모순이 없다. 양수에서 만족하는 사칙 연산의 법칙들이 음수에서도 별 특이 변화없이 만족하도록 확장하려 하면, 음수와 음수의 곱은 양수가 되어야 한다.
싱겁게도 정답이 위와 같다. 사칙연산의 일반적인 양수에서의 패턴을 그대로 유지하려면 그래야 한다.
이 외에도 덧셈의 반대연산인 뺄셈, 곱셈의 반대연산인 나눗셈, 그리고 곱셈의 거듭연산인 지수와 그 반대 연산인 로그 등으로 확장되고 그리고 그 연산들이, 미지수 x를 구하는 대수학에서 분수와 무리수, 허수를 낳게 되듯이 이 대칭체계는 그렇게 무모순을 만들기 위해 계속해서 개념들이 탄생하게 된다. 인간이 상상할 수 없는 방식과 숫자가 계속 탄생하게 되는 것이라고 볼 수 있다. 그렇게 음수를 음수번 반복하면, 다시 양수가 나타나야만 이 숫자 체계가 완전해진다. 허수는 인간의 개념속에 존재하지 않지만 그런 특성을 지녀야만 수 체계가 모순없이 구성된다. 누군가는 아마 이런 음수 곱셈 개념들이 개념이 머리속에 맑게 당연할 수도 있겠다. 그런데 많은 사람들이 그러지 못하고 그냥 그 특성으로 외워야될 수도 있을 수 있는 것이다. 그것이 유일하게 모순되지 않는 방법이라고.
'순수수학' 카테고리의 다른 글
| 소수와 대칭, 대칭은 또다른 더 작은 대칭으로 대치될 수 있는가? (0) | 2023.02.18 |
|---|---|
| 엔트로피와 무한, 그 안에서의 질서와 생명현상 (0) | 2022.12.04 |
| 대칭의 심연, 모든 수는 대칭에서 탄생한다 2 (0) | 2022.11.09 |
| 카오스 이론 소개, 엑셀로 알아보자 (0) | 2022.07.31 |
| 파이(pi)와 자연상수 e에 대하여, 오일러 공식과 함께 알아보기 (0) | 2022.07.30 |
